实验语音学常用软件入门•SPSS 相关性分析
概论
什么是相关性分析?
相关性分析是一种统计方法,用于评估两个或多个变量之间的关系强度和方向。它帮助我们理解变量之间的关联程度,即一个变量的变化如何影响另一个变量的变化。在相关性分析中,我们通常关注两个方面:
- 关系强度:相关性分析告诉我们变量之间的相关程度有多高。如果两个变量之间的相关性较强,那么它们的变化趋势会更加一致。
- 关系方向:相关性分析还能指示变量之间的关系方向。这意味着当一个变量增加时,另一个变量是增加还是减少,或者它们之间存在无明显关系。
所以,相关系数有以下几种情况:
- 正相关(Positive correlation):当相关系数接近1时,表明两个变量之间存在正的关联。这意味着一个变量的值增加时,另一个变量的值也倾向于增加。相关系数越接近1,表明这种正向关联越强。
- 负相关(Negative correlation):当相关系数接近-1时,表明两个变量之间存在负的关联。这意味着一个变量的值增加时,另一个变量的值倾向于减少。相关系数越接近-1,表明这种负向关联越强。
- 不相关(No correlation):当相关系数接近0时,表明两个变量之间没有明显的单调关联。
相关性分析在语言学研究中的应用
在语言学研究中,相关性分析是一种常用的统计方法,可以用来探索各种语言现象之间的关系。一些典型的应用包括:
- 语言习得:研究语言习得过程中各种因素(如年龄、学习环境等)与语言能力之间的关系。
- 语言使用:分析语言使用频率与不同社会文化背景、社会地位或年龄段之间的相关性,以了解语言使用的偏好和习惯。
- 语言变化:研究语言变化趋势与时间、地理位置或社会文化因素之间的关系,以便更好地理解语言演变和发展规律。
相关性分析的方法
1. 皮尔逊相关系数 (Pearson's correlation coefficient)
- 介绍:皮尔逊相关系数衡量的是两个变量之间的线性相关性。系数的取值范围从-1到1。系数为1表示完全正相关,-1表示完全负相关,而0表示没有线性相关。
- 适用情况:适用于两个变量均为连续数据,且大致呈正态分布,且符合方差齐性。此外,两个变量之间的关系应当是线性的,即变量的变化趋势应当是直线形态的。
2. 斯皮尔曼等级相关系数 (Spearman's rank correlation coefficient)
- 介绍:斯皮尔曼相关系数是一种非参数的相关性检验方法,它通过将数据转换为等级(排名)来计算两个变量之间的单调相关性。
- 适用情况:适合用于评估两个变量是否存在单调关系,即无论是线性还是非线性的关系。斯皮尔曼相关性检验适用于非正态分布的数据,或者当数据含有离群值、秩次数据时。
3. 肯德尔秩相关系数 (Kendall's tau coefficient)
- 介绍:肯德尔相关系数也是一种非参数的相关性检验方法,它基于一对数据之间的一致性和不一致性对进行评估。肯德尔系数测量的是变量之间的关联强度。
- 适用情况:与斯皮尔曼相关系数类似,肯德尔相关性检验适用于连续或有序分类变量。特别适用于样本量较小,或数据中存在许多 tied ranks(即多个观察值有相同的秩次)的情况。
实验材料
假设我们要探索的是语言能力与年龄、学习时间以及语言环境的关系。以下是具体的数据集描述:
- 年龄(Age):参与者的年龄,单位为年。一共50名参与者。
- 学习时间(StudyHours):每周用于学习语言的时间,单位为小时。
- 语言环境得分(LanguageExposureScore):这是一个量化参与者日常生活中使用或接触到的语言数量的分数,分数越高,表示接触的语言越多。
- 语言能力得分(LanguageProficiencyScore):通过标准化测试评估的语言能力,分数范围从0到100。
| Age | StudyHours | LanguageExposureScore | LanguageProficiencyScore |
|---|---|---|---|
| 56 | 15 | 43 | 71 |
| 46 | 18 | 42 | 100 |
| 32 | 5 | 57 | 62 |
| 60 | 19 | 32 | 49 |
| 25 | 9 | 71 | 73 |
| …… | …… | …… | …… |
操作步骤
1.导入数据
确保数据已经被正确导入到SPSS中。数据应当是清洗后的,没有缺失值,并且所有的变量都正确地定义了其测量水平(比如,标度、序数)。
2.观察线性关系
-
点击图形➡️旧对话框➡️散点图/点图 。在弹出框中,点击简单散点图。

-
在弹出框中,将要探究的两个变量分别放入X轴与Y轴。
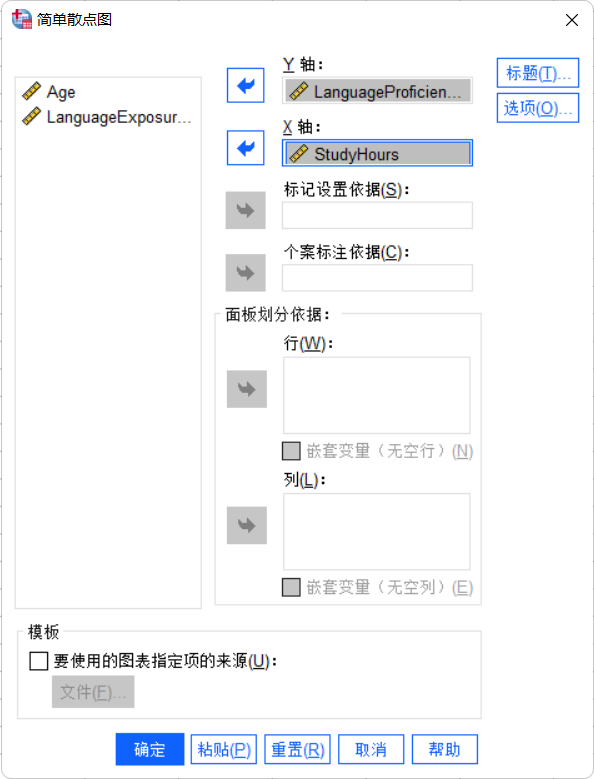
-
查看散点图。(下面的图不是通过SPSS生成,但是内容一致。)
-
学习时间与语言能力得分:展示线性关系,适合皮尔逊相关性。

-
年龄与语言能力得分:可能适合斯皮尔曼或肯德尔相关性。

3.打开相关性分析选项
- 启动SPSS,加载你的数据集。
- 在菜单栏中选择“分析”(Analyze)。 指向“相关”(Correlate),选择“双变量...”(Bivariate…)。这将打开一个对话框,用于设置相关性分析。
4.选择相关性类型和变量
在“双变量相关性”对话框中:
- 选择变量:从左侧的变量列表中选择你想要分析的变量,点击中间的箭头将它们移至右侧的“变量”框。
- 选择相关性类型:
- 可以同时选择多种相关性类型进行比较。
- 标记“两尾”或“一尾”:通常选择“两尾”测试,因为它考虑了正相关和负相关的可能性。
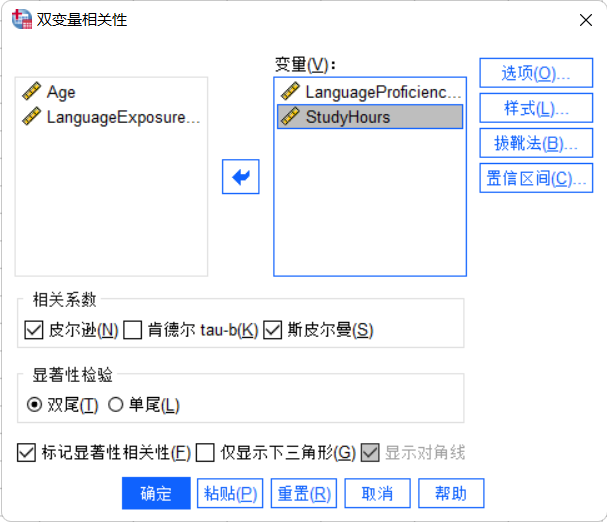
点击“确定”(OK)按钮运行相关性分析。SPSS将在输出窗口中显示结果。
5.解读输出结果
学习时间与语言能力得分
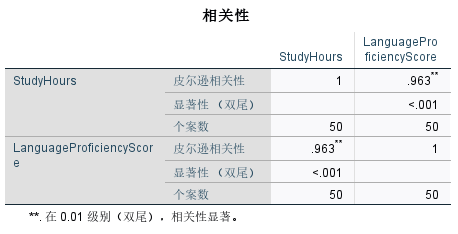
- 皮尔逊相关系数:两个变量之间的相关系数为0.963,表明存在极强的正相关关系。这意味着随着学习时间的增加,语言能力得分也显著增加。
- 显著性水平:双尾显著性为0.000,这表明这个相关性在统计上非常显著。
文字叙述:
为了探索“每周学习时间”(StudyHours)与“语言能力得分”(LanguageProficiencyScore)之间的关系,进行了皮尔逊相关性分析。结果显示两个变量之间存在极强的正相关关系(r = 0.963, p < 0.01)。这个结果表示,学习时间对语言能力有显著的正向影响。对于教育和教学研究者,这可能意味着增加学习时间可以有效提高语言能力。然而,进一步的研究需要考虑其他可能影响语言能力的因素。
年龄与语言能力得分

- 相关系数:斯皮尔曼相关系数为-0.116,表明存在负相关性,但这个相关系数较低,暗示两个变量之间没有显著的单调关系。
- 显著性水平:显著性(双尾)为0.424,这意味着这个相关性在统计上不显著。即,年龄与语言能力得分之间的负相关可能是随机产生的。
为了探索“年龄”(Age)与“语言能力得分”(LanguageProficiencyScore)之间的关系,进行了斯皮尔曼相关性分析。结果显示两个变量之间的相关系数为-0.116,表明存在负相关性,但在统计上不显著(p = 0.424)。
这个结果说明,年龄与语言能力得分之间没有显著的单调关系。负相关性可能暗示年龄增加时语言能力下降,但这个趋势可能并不明显。因此,进一步研究需要考虑其他可能影响语言能力的因素。
操作步骤-偏相关分析
偏相关分析是用来测量在控制其他变量影响后,两个变量之间的相关性。在SPSS中,偏相关分析可以帮助你了解在排除干扰变量影响后,主要变量之间的关系。以下是SPSS中进行偏相关分析的详细步骤。
1.准备数据
确保你的数据已经导入SPSS,且数据已正确编码和清洗。你需要选择要分析的主要变量和控制变量。
2.打开偏相关分析选项
在菜单栏中选择“分析”(Analyze),指向“相关”(Correlate)。选择“偏相关”(Partial...)。这将打开一个对话框,用于设置偏相关分析。
3.选择主要变量和控制变量
在“偏相关”对话框中:
- 选择主要变量:从左侧的变量列表中选择你想要分析的主要变量,并将它们移动到右侧的“变量”框。
- 选择控制变量:将要控制的变量移动到中间的“控制变量”框。这些变量是你想在分析中控制其影响的因素。
- 选择相关性类型:通常,默认是皮尔逊相关性。如果你的数据是序数数据或不满足正态性要求,可以选择斯皮尔曼相关性。
- 标记“两尾”或“一尾”:一般选择“两尾”,以考虑相关性的正负方向。
- 缺失值处理:选择“成对”(Pairwise)或“列表删除”(Listwise)来处理缺失值。
4.运行分析
点击“确定”(OK)按钮,SPSS将运行偏相关分析。结果将在输出窗口中显示。
5.解读输出结果

在控制“年龄”变量后,皮尔逊相关性结果显示了以下主要发现:
- StudyHours与LanguageProficiencyScore:相关性为0.963,显著性为0.000,表明在控制年龄影响后,学习时间与语言能力得分之间仍存在极强的正相关关系,并且在统计上显著。显著性水平的结果表明,这个相关性在统计上是显著的,可能性小于0.01。
这个结果暗示,尽管年龄可能影响学习时间和语言能力,但它对学习时间与语言能力之间的正相关关系并没有显著影响。
为了探索“每周学习时间”(StudyHours)与“语言能力得分”(LanguageProficiencyScore)之间的关系,在控制“年龄”(Age)的情况下,进行了偏相关分析。结果显示,两个变量之间的相关性为0.963,显著性为0.000,表明在控制年龄影响后,学习时间与语言能力得分之间仍然存在极强的正相关关系。这个结果表明,尽管年龄可能影响学习时间和语言能力,但它不会显著改变学习时间与语言能力之间的关联。
余论
p值的等级
| p值区间 | 显著性水平 | 星号表示法 | 论文中的描述方式 |
|---|---|---|---|
| p > 0.05 | 不显著 | 无星号 | “差异不显著”或“没有显著差异” |
| p ≤ 0.05 | 显著 | * | “显著”或“存在显著差异” |
| p ≤ 0.01 | 高度显著 | ** | “高度显著”或“差异显著性更高” |
| p ≤ 0.001 | 极其显著 | *** | “极其显著”或“差异显著性极高” |
相关性分析方法的选择
选择正确的相关性检验方法对于获取有效、可靠的研究结果至关重要。皮尔逊、斯皮尔曼和肯德尔相关性检验各有其特点和适用场景。
相关系数的强弱
相关系数的大小表征变量之间关联的强度。通常,相关系数(如皮尔逊相关系数)的绝对值越接近1,表明变量间的关联越强;越接近0,表明关联越弱。但“小”或“大”的具体数值并没有严格的标准,它们在不同的学科和研究领域中可能有不同的解释。不过,可以参考以下一些常见的基准来解读相关系数的大小:
- 弱相关:0.1 到 0.3 或 -0.1 到 -0.3
- 中等相关:0.3 到 0.7 或 -0.3 到 -0.7
- 强相关:0.7 到 1.0 或 -0.7 到 -1.0
斯皮尔曼和肯德尔相关系数也可以使用类似的范围来判断相关的强度,虽然它们是非参数的相关系数,通常用于评估变量间的单调关系,不一定是线性关系。
注意事项
- 研究领域的不同:在某些学科,如社会科学或心理学,即使是0.2到0.3的相关系数也可能被视为有意义的,因为影响行为的因素往往多而复杂。而在物理或生物科学中,更强的相关(如大于0.5)可能才被视为重要。
- 样本大小的影响:较大的样本使得即使是小的相关系数也可能统计显著。因此,解读相关系数时也需要考虑样本大小。
- 数据特性:数据的分布和质量(如是否存在离群值)也可能影响相关系数的大小。
绘制相关性矩阵图及热力图
在进行多个变量的相关性分析的时候,可以在论文中绘制这样的矩阵表格。
| StudyHours | LanguageProficiencyScore | Age |
|---|---|---|
| StudyHours | 1 | 0.963** |
| LanguageProficiencyScore | 0.963** | 1 |
| Age | -0.112 | -0.138 |
注:双尾检验在0.01级别显著。
当然,如果掌握其他的软件及语言,如Python和R,也可以以下的生成热力图,但本系列教程不做讲解。
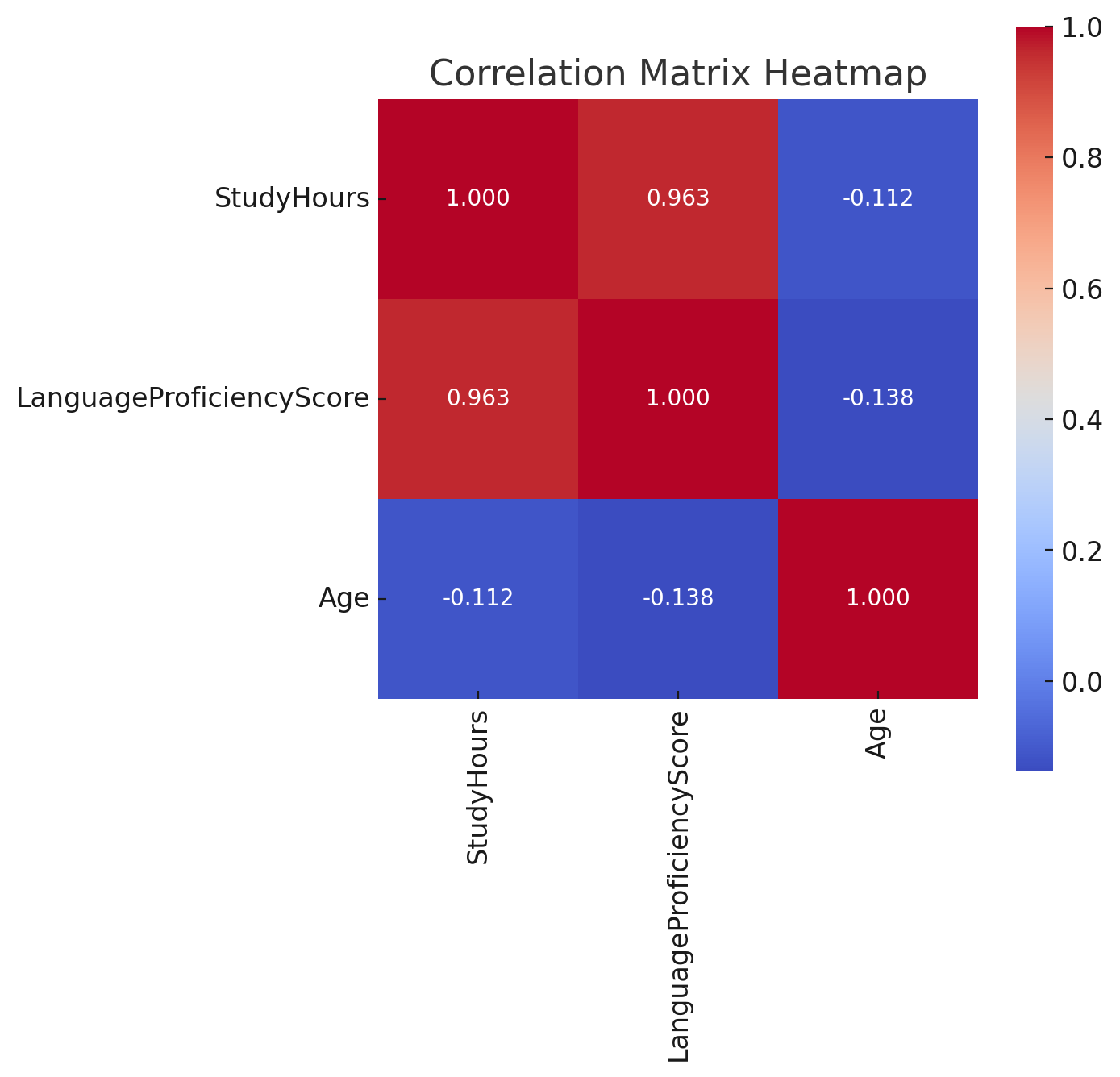
.png)