实验语音学常用软件入门•SPSS 非参数检验
编辑概论
非参数检验(Nonparametric Tests),也称分布无关检验,是一类统计检验方法,与参数检验(如t检验、ANOVA等)不同。非参数检验的特点是不需要假设数据符合某种特定的概率分布(如正态分布),因此在数据分布未知或数据不符合正态性假设时,非参数检验是理想的选择。
非参数检验的主要优点包括:
- 适用范围广:可以用于不同数据分布类型、样本量较小的数据。
- 对异常值的敏感性较低:与参数检验相比,非参数检验对异常值的影响较小。
- 无需数据转换:非参数检验通常不需要对数据进行转换,以适应分布假设。
但非参数检验也有一些缺点,例如:
- 统计功效较低:相对于参数检验,非参数检验的统计功效可能较低。
- 难以处理多因素设计:非参数检验在处理复杂的多因素实验设计时,可能不如参数检验。
常见的非参数检验方法
| 参数方法 | 非参数方法 |
|---|---|
| 独立样本T检验配对样本T检验 | Mann-Whitney U检验(独立样本)Wilcoxon符号秩检验(配对样本) |
| 单因素ANOVA多因素ANOVA | Kruskal-Wallis H检验(单因素)Friedman检验(多个相关样本) |
| 皮尔逊相关系数 | 斯皮尔曼等级相关系数肯德尔等级相关系数 |
非参数检验包括多种方法,常见的有:
- Mann-Whitney U检验:用于比较两组独立样本的中位数,类似于独立样本t检验。
- Wilcoxon符号秩检验:用于比较两组相关样本的中位数,类似于配对样本t检验。
- Kruskal-Wallis H检验:用于比较三组或多组独立样本的中位数,类似于单因素ANOVA。
- Friedman检验:用于比较三组或多组相关样本的中位数,类似于重复测量ANOVA。
实验材料
数据1说明
- 训练方法:A, B, C三种方法
- 性别:男性、女性
- 发音准确性:使用某种量化方式评分(1-100分)
以下是部分数据的展示:
| Participant_ID | Method | Gender | Pronunciation_Accuracy |
|---|---|---|---|
| 1 | A | Male | 88 |
| 1 | B | Male | 78 |
| 1 | C | Male | 64 |
| 2 | A | Female | 92 |
| 2 | B | Female | 57 |
| 2 | C | Female | 70 |
| 3 | A | Male | 88 |
| 3 | B | Male | 68 |
| 3 | C | Male | 72 |
| 4 | A | Female | 60 |
| 4 | B | Female | 60 |
| 4 | C | Female | 73 |
检验方法
- Mann-Whitney U检验:比较男性和女性在同一训练方法下的发音准确性差异。
- Kruskal-Wallis H检验:比较三种训练方法在整体上对发音准确性的影响。
数据2说明
该数据与下一篇《SPSS ANOVA检验2》数据集相同,本篇里假设此数据集不满足参数检验的要求,采用非参数检验。
检验方法
- Friedman检验:比较同一参与者在三种方法下的评分差异。
操作步骤
Mann-Whitney U检验
这个检验用来比较两个独立样本的分布。假设我们比较男性和女性在方法A下的评分。
-
转到
分析->非参数检验->独立样本...。
-
在弹出窗口中,将
Pronunciation_Accuracy拖到“检验字段”框。将Gender拖到“组”框,设置组值(例如,1 = Male, 2 = Female)。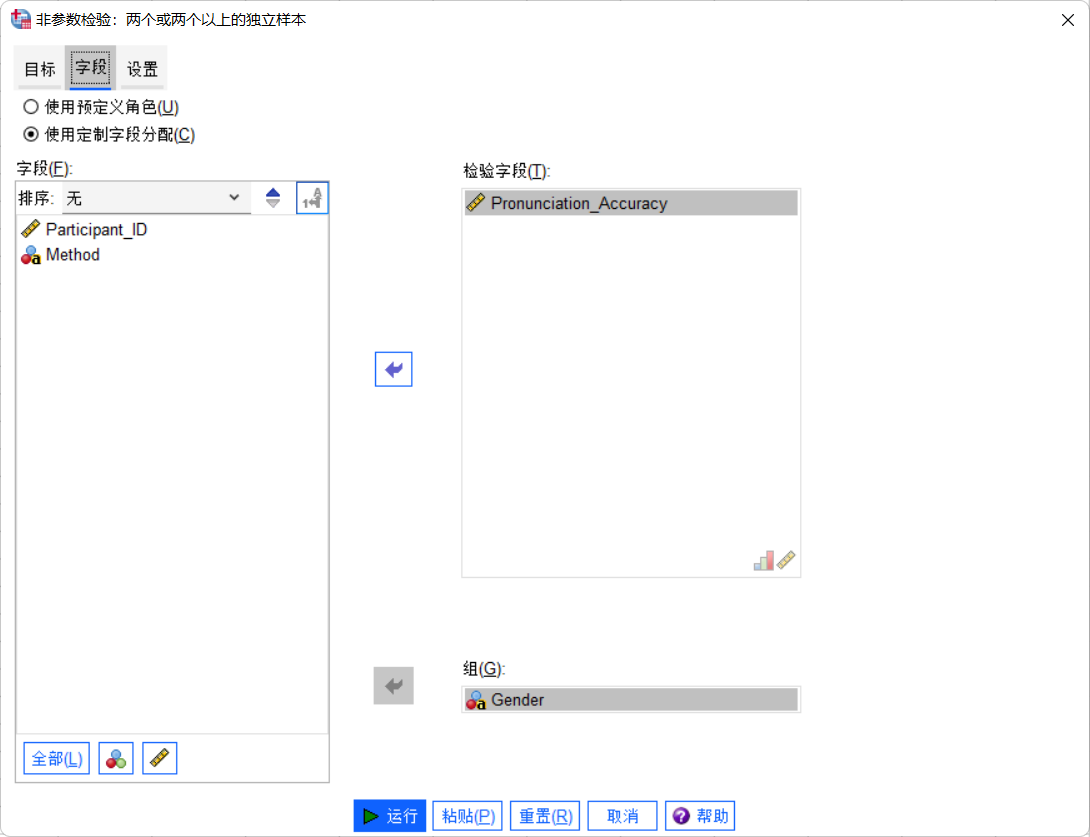
-
点击“确定”。
结果解读

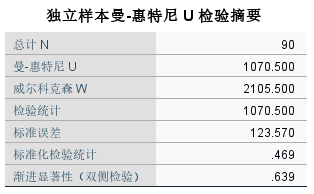
文字叙述
在研究中,我们探讨了性别是否影响发音准确性。为此,我们应用了独立样本曼-惠特尼 U 检验来比较两个性别组的发音准确性分布。分析结果显示,Z=0.469,p=0.639>0.05。这表明在性别对发音准确性的影响上,两个组之间没有统计学上的显著差异。因此,我们保留原假设,认为在性别分类上,发音准确性的分布是相似的。
Kruskal-Wallis H检验
这个检验用来比较三个或更多独立样本的分布。假设我们比较三种方法对发音准确性的影响。
- 点击
分析->非参数检验->独立样本...。
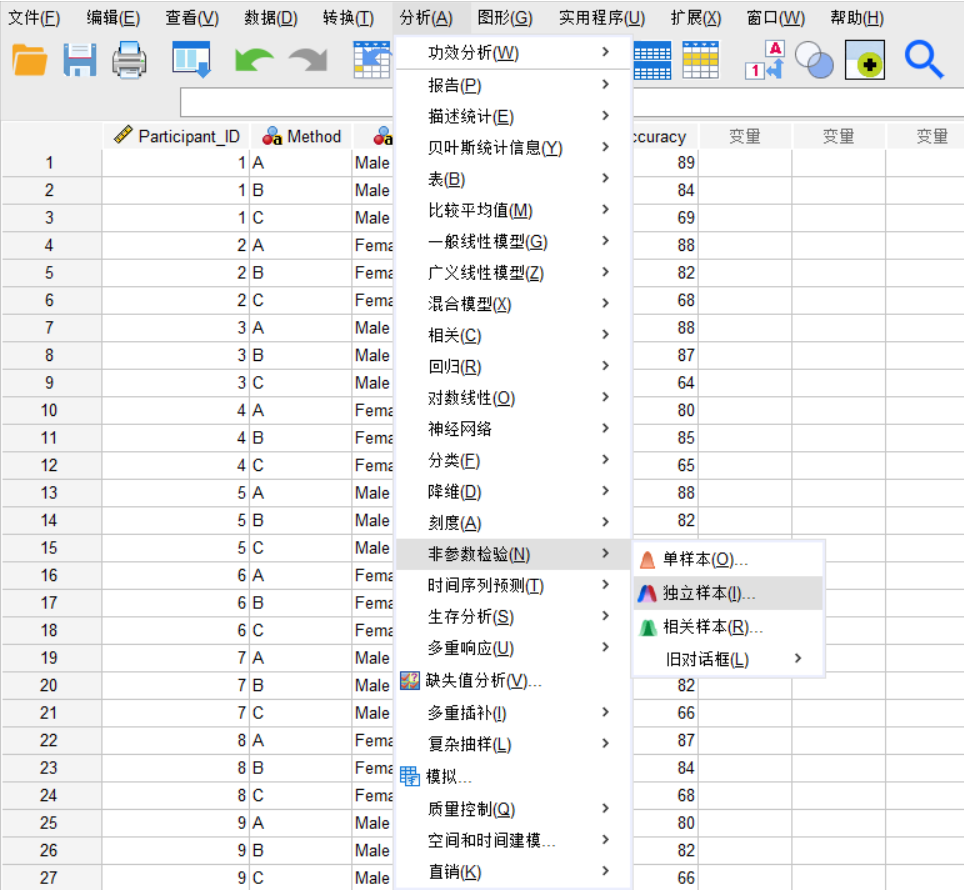
- 选择
Pronunciation_Accuracy作为“检验字段”,Method作为“组”。
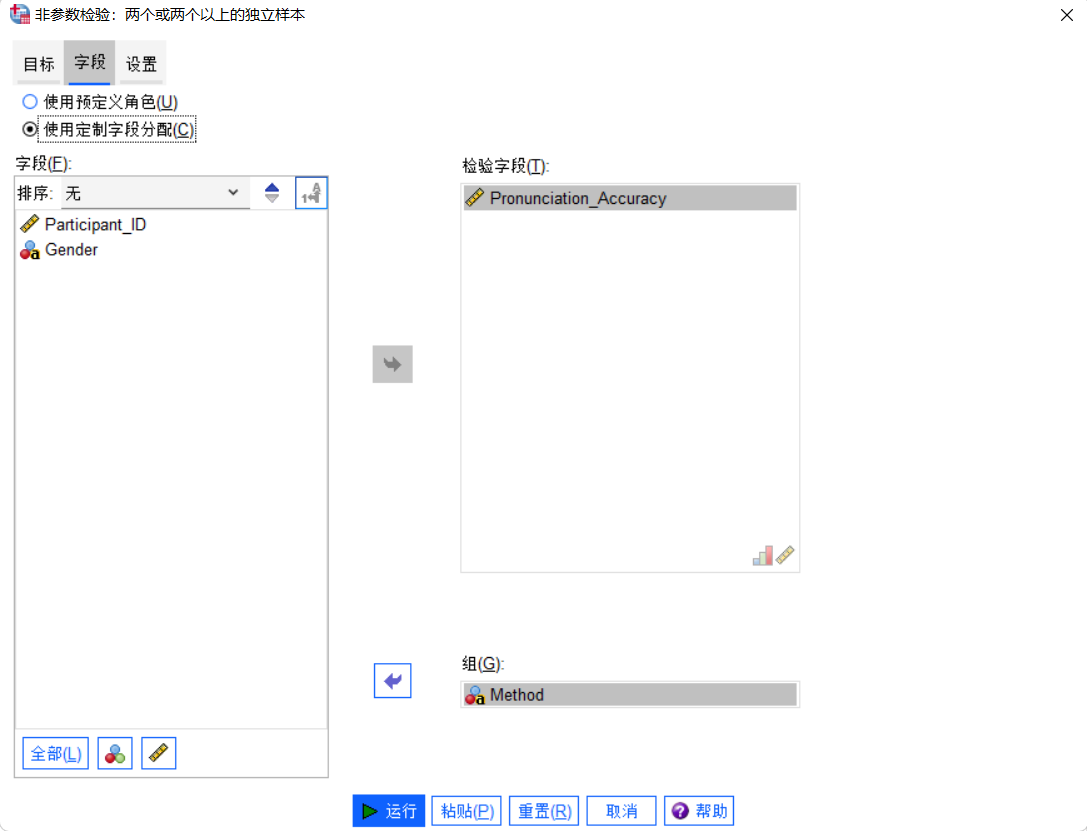
- 点击“运行”。
注意:这些步骤和前面的xxx检验完全相同,软件会自动根据组别数量采取相应的方法。
结果解读

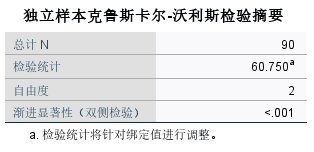
- 克鲁斯卡尔-沃利斯检验:
- 检验不同方法(Method)对于发音准确性(Pronunciation_Accuracy)分布是否有显著差异。
- 结果:检验统计量为60.750,自由度为2,渐进显著性(双侧检验)为0.000。由于显著性水平为0.000,远小于设定的显著性水平0.050,我们拒绝原假设,即不同的方法在发音准确性上的分布是有显著差异的。
![[Pasted image 20240503090727.png]]
-
成对比较:
- C-B:显著性为.000,调整后显著性为.000,表明C方法和B方法在发音准确性分布上有显著差异。
- C-A:显著性为.000,调整后显著性为.000,表明C方法和A方法在发音准确性分布上有显著差异。
- B-A:显著性为.300,调整后显著性为.901,表明B方法和A方法在发音准确性分布上没有显著差异。

- 根据箱线图,我们也可以观察到:
- 方法C的中位数最低,整体分布也明显低于其他两种方法,表明使用方法C的学生在发音准确性上的表现较差。
- 方法A和方法B的发音准确性中位数相近,且分布范围(即箱体大小)相似,表明这两种方法在发音准确性上的效果较为接近。
- 存在一些较为极端的数据点,但整体来看,异常值不多。
文字叙述
本研究使用Kruskal-Wallis H检验来分析不同教学方法对学生发音准确性的影响。结果表明,这些教学方法对发音准确性的影响存在显著差异(𝐻=60.750,𝑑𝑓=2,𝑝<.001)。在成对比较中,方法C与方法A(𝑍=7.208,𝑝<.001)和方法C与方法B(𝑍=6.172,𝑝<.001)之间显示出显著差异,而方法B与方法A之间的差异不显著(𝑍=1.036,𝑝=.901)。这些结果表明不同的教学方法对提高学生的发音准确性具有不同的效果。
Friedman检验
这个检验用来比较三个或更多相关样本的分布。我们将比较同一参与者在三种方法下的评分差异。
-
点击“分析” > “非参数检验” > “相关样本...”。
-
在弹出的“相关样本的非参数检验”窗口中: 将“Month0”, “Month1”, “Month3”依次拖入“测试变量”框中。
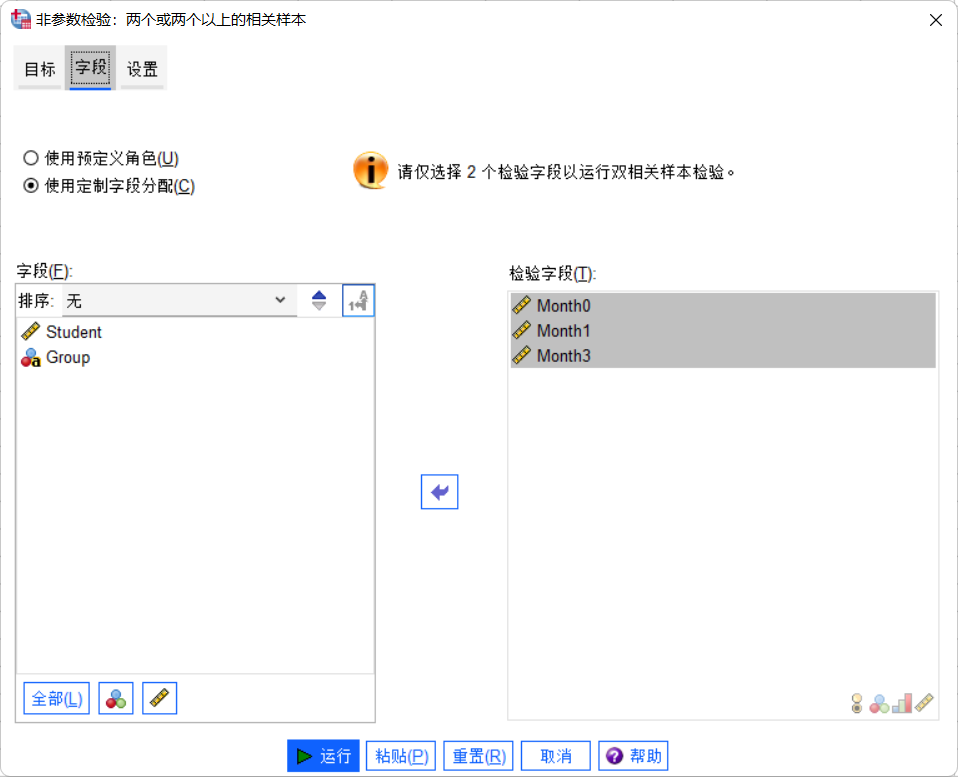
-
点击“确定”按钮开始检验。
结果解读

- 解释: Friedman 检验统计量为 59.513,自由度为 2,显著性水平为 .000。这进一步证实了我们拒绝原假设,即三个时间点的词汇量分布不同。
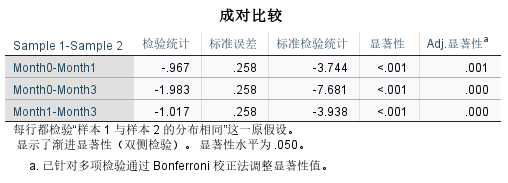
成对比较显示每两个时间点之间的分布显著不同。Bonferroni 校正后的显著性值进一步支持了这种差异。具体结果如下:
- Month0 与 Month1 之间的检验统计量为 -3.744,显著性为 .001,表示 Month0 和 Month1 的分布显著不同。
- Month0 与 Month3 之间的检验统计量为 -7.681,显著性为 .000,表示 Month0 和 Month3 的分布显著不同。
- Month1 与 Month3 之间的检验统计量为 -3.938,显著性为 .000,表示 Month1 和 Month3 的分布显著不同。
文字叙述
经检验,数据符合非参数检验要求。为了评估不同时间点之间的差异,采用了弗莱德曼双向检验进行分析。检验结果显示,各时间点之间存在显著性差异(χ²(2) = 59.513, p < 0.001)。为进一步探讨具体时间点之间的差异,本研究进行了成对比较分析,结果表明,三个时间点之间的差异均具有统计学显著性(Bonferroni 校正),这表明所研究的变量在不同时间点上的变化显著。
余论
非参数检验和参数检验
-
参数检验:
- 参数检验是基于一些关于数据分布的特定假设,通常假设数据来自某个已知的分布(如正态分布)。
- 这类检验需要样本数据满足一定的条件,如独立同分布、具有一定的分布形式(例如正态性)等。
- 常见的参数检验包括t检验(用于样本均值的比较)、方差分析(比较多个组的均值差异)等。
-
非参数检验:
- 非参数检验不依赖于数据的分布假设,因此它们通常被用于那些不能满足参数检验所需正态分布或其他分布假设的数据。
- 这类检验适用于序数数据或名义数据,以及不能确保数据分布的情况。
关系与适用场景
- 应用范围:当数据满足正态分布假设时,参数检验通常更为精确,因为它利用了更多关于数据分布的信息。当数据不满足这些假设时,非参数检验提供了一种替代方案。
- 统计效力:在数据确实符合参数检验的假设时,参数检验的统计效力(即发现实际存在效应的能力)通常优于非参数检验。但如果数据违反了参数检验的假设,非参数检验则可能更为可靠。
- 灵活性:非参数检验由于较少的假设要求,对数据的形态和分布的要求不严,因此在实际应用中更为灵活。
- 0
- 0
-
分享
.png)