实验语音学常用软件入门•SPSS ANOVA检验2
概论
什么是重复测量方差分析?
在语言学研究中,重复测量方差分析(Repeated Measures ANOVA)是一种强有力的统计工具,用于检测同一组被试在不同条件或时间点的均值是否存在显著差异。与独立样本ANOVA不同,它考虑了同一被试之间的相关性,从而提供更准确的结果。
实验数据
数据准备
假设我们进行了一项实验,研究两种新的语言教学方法A与B对学生词汇量的影响。我们在三个月的时间内,对30名学生(分成A组与B组)在0个月、1个月和3个月的词汇量进行了测量。局部数据如下:
| Student | Group | Month0 | Month1 | Month3 |
|---|---|---|---|---|
| 1 | A | 50 | 66 | 87 |
| 2 | A | 55 | 62 | 92 |
| 3 | A | 46 | 66 | 78 |
| 4 | B | 48 | 53 | 85 |
| 5 | B | 48 | 63 | 85 |
操作步骤
导入数据
- 启动 SPSS。
- 点击“文件” > “打开” > “数据”。
- 在弹出的窗口中,选择“文件类型”为“CSV (*.csv)”(本次数据格式为csv),然后找到并打开文件。
检查数据
- 确认数据已正确导入,列名分别为“Student”, “Group”, “Month0”, “Month1”, “Month3”。
- 确认每个变量的类型,其中“Group”应为“字符串”,“Month0”, “Month1”, “Month3”应为“数值”。
定义重复测量因子
-
点击“分析” > “一般线性模型” > “重复测量...”
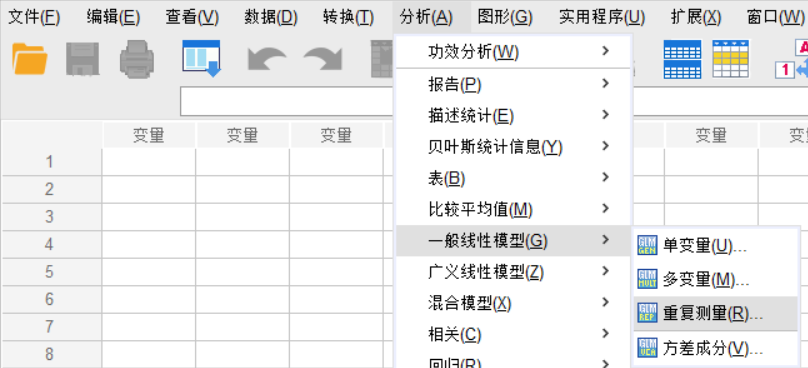
-
在“重复测量定义”窗口中:
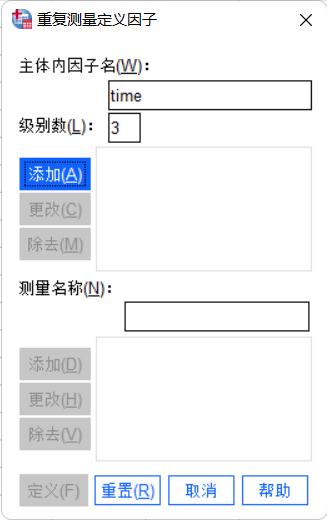
-
在“主体内因子名(W)”框中输入
Time,这里可以自由命名,便于分析即可。 -
在“级别数(L)”框中输入
3。 -
点击“添加(A)”。
-
点击“定义(F)”。
指定测量变量
-
在弹出的“重复测量”窗口中,将
Month0,Month1,Month3依次拖入“Time(3)”下面的三个框中。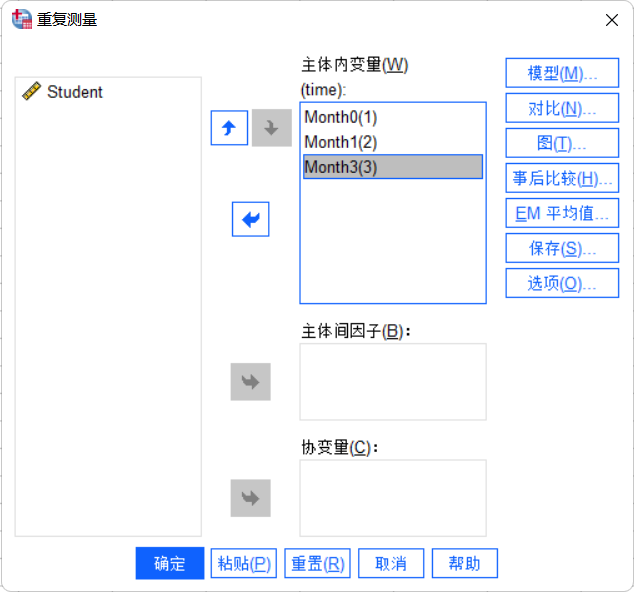
添加主体间因子
-
在“主体间因子”框中,将“Group”拖入其中。
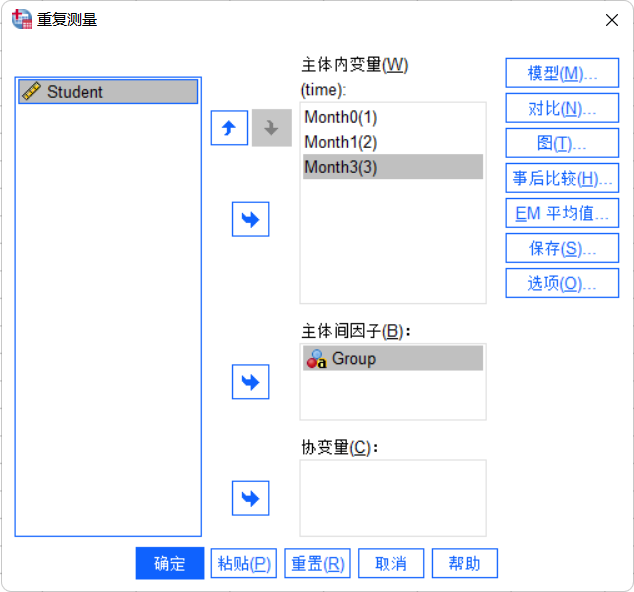
设置分析选项
-
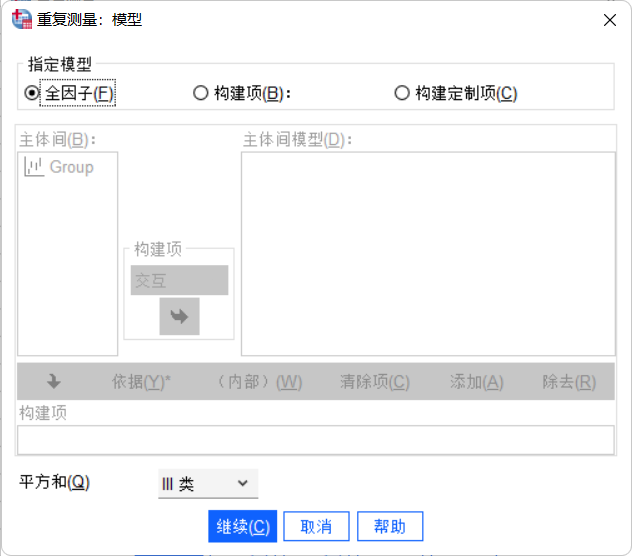
点击“模型...”按钮,选择“全因子”,点击“继续”。
-
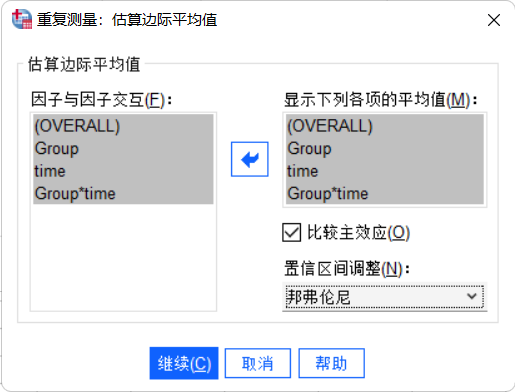
点击“EM平均值”按钮,选择需要分析的事后比较项,勾选适当的事后比较方法(如Bonferroni),点击“继续”。
-
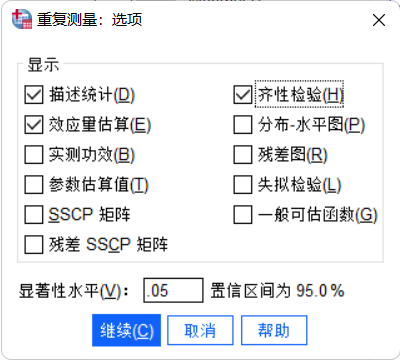
点击“选项...”按钮,勾选“描述性统计”、“估计边际均值”、“效应大小”等选项,点击“继续”。
修改代码与运行分析
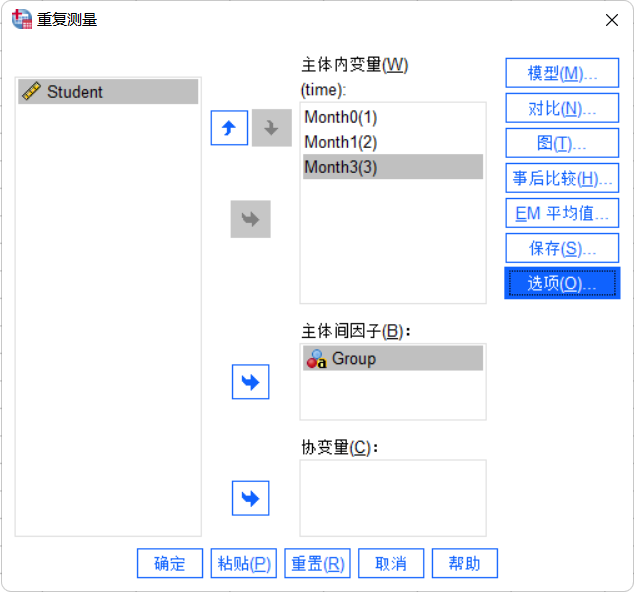
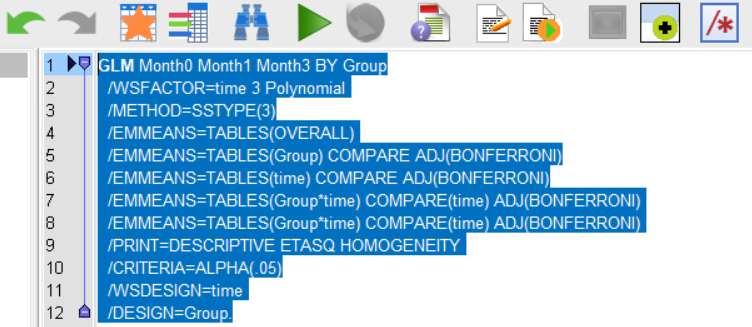
- 确认设置无误后,点击“粘贴”按钮(不是点击“确定”)。因为我们要进行简单效应分析,在SPSS里需要手动修改代码,这一点与之前的单因素与双因素ANOVA教程相同。
修改前:
GLM Month0 Month1 Month3 BY Group
/WSFACTOR=time 3 Polynomial
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(OVERALL)
/EMMEANS=TABLES(Group) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(time) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(Group*time)
/PRINT=DESCRIPTIVE ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/WSDESIGN=time
/DESIGN=Group.
修改后:
GLM Month0 Month1 Month3 BY Group
/WSFACTOR=time 3 Polynomial
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(OVERALL)
/EMMEANS=TABLES(Group) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(time) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(Group*time) COMPARE(time) ADJ(BONFERRONI) #此行修改,表示在控制group的情况下,分析不同time的简单效应。
/EMMEANS=TABLES(Group*time) COMPARE(time) ADJ(BONFERRONI) #此行新增,表示在控制time的情况下,分析不同group的简单效应。
/PRINT=DESCRIPTIVE ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/WSDESIGN=time
/DESIGN=Group.
- 选中代码片段,点击绿色的运行按钮。
解释结果
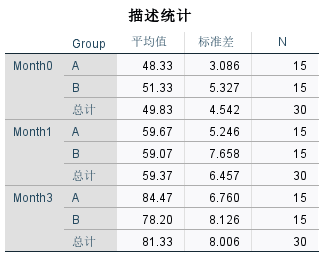
描述性统计
- 显示每个时间点和每个组别的平均分和标准差。
方差齐性检验
- 协方差矩阵的博克斯等同性检验: 主要用于多因素方差分析和重复测量方差分析,用于验证不同组的协方差矩阵是否相等。如果涉及多个因变量或需要进行多元方差分析,一般查看这个检验。
- 误差方差的莱文等同性检验: 用于单因素方差分析中,验证不同组的误差方差是否相等。如果进行的是单一因变量的方差分析,莱文检验更加适用。
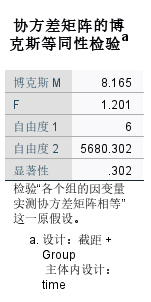
由于 p =0.302 >0.05,这表明不同组的协方差矩阵相等,满足重复测量方差分析的假设。因此,可以进行进一步的多变量分析。
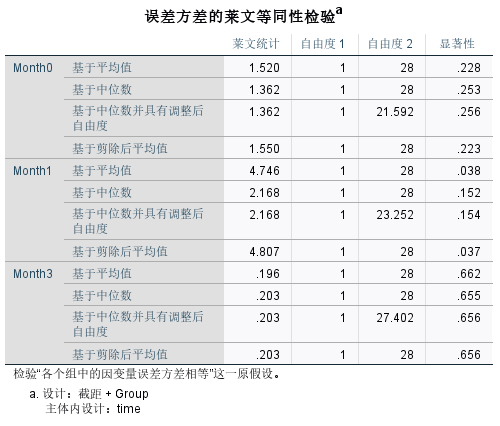
- Month0:基于平均值的显著性 p = .228 > 0.05,表明方差齐性假设成立。
- Month1:基于平均值的显著性 p = .038 < 0.05,表明方差齐性假设不成立。
- Month3: 基于平均值的显著性 p = .662 > 0.05,表明方差齐性假设成立。
对于 Month1,由于显著性 p < 0.05,表示不同组的误差方差不相等,这可能会影响方差分析结果的解释。
球形度检验与后续检验结果查看
球形度检验
- Mauchly’s Test of Sphericity: 检验球形假设是否成立。
- 如果球形度检验P<0.05,需要看多变量检验结果或者主体内效应检验的校正结果。
- 如果球形度检验P>0.05,看主体内效应检验-假设球形度结果。
在本次试验中,Mauchly 球形度检验结果显著(p < 0.05),表明球形假设被违反,因此需要使用校正结果(如Greenhouse-Geisser校正)。
主体内效应
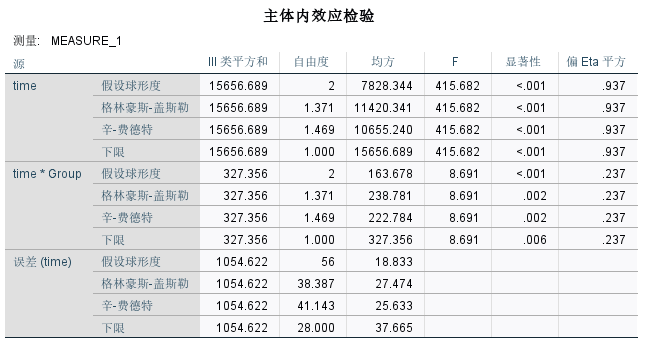
主体内效应检验显示时间因素和时间与组别的交互作用在统计上显著(p < 0.05)。
多变量检验
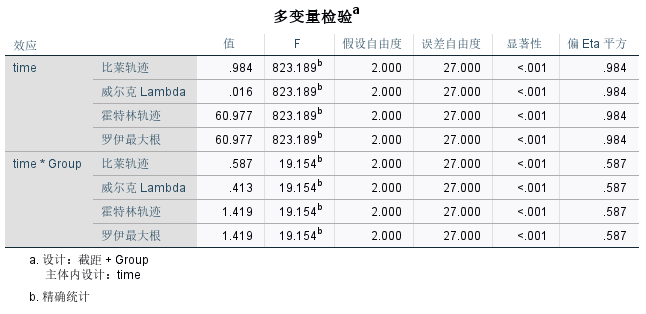
多变量检验结果表明,时间因素(time)和时间与组别交互作用(time * Group)在统计上显著(p < 0.05)。
主体间效应
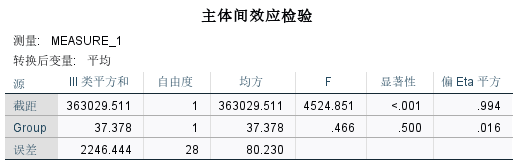
主体间效应检验显示组别因素对词汇量的影响在统计上不显著(p > 0.05),表明两种教学方法在整体词汇量提升上没有显著差异。
事后比较与简单效应
一旦交互效应存在统计学意义,必须看简单效应,不能以主效应结果为准,因为有可能简单效应与主效应结果相互矛盾。关于交互效应与简单效应的讨论,请回看《ANOVA1》
因为该实验涉及的事后比较表格过多,仅举其中一例来分析。分析方式与前文单因素和双因素anova相同,不再赘述。
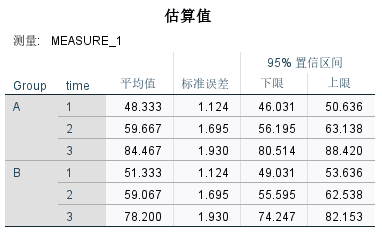
这个表格显示了两组学生在不同时间点的估算平均词汇量。
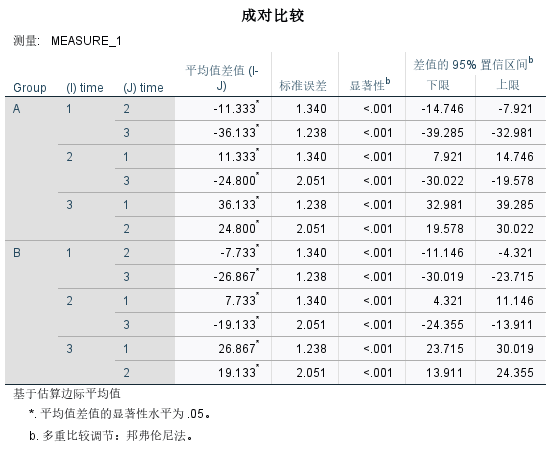
成对比较显示在每个组别内的不同时间点之间的平均词汇量差异均在统计上显著(p < 0.05),并且两组的增长模式有所不同。
实验结论
如果全部完成分析,可以得出以下结论:
- 总体平均值: 学生的平均词汇量为 63.511,区间为 61.577 至 65.445。
- 组别效应: 虽然组别 A 和 B 的平均词汇量有所不同,但这种差异在统计上不显著(p = 0.500)。
- 时间效应: 随着时间的推移,学生的词汇量显著增加,每个时间点之间的差异在统计上显著(p < 0.05)。
- 交互作用: 组别与时间的交互作用在统计上显著,表明不同教学方法在不同时间点的效果有所不同。
这些结果表明,尽管两种教学方法在整体词汇量提升上没有显著差异,但随时间的推移,学生的词汇量显著增加,并且不同方法在不同时间点的效果有所不同。这可能意味着教师可以根据不同时间点的需要调整教学策略,以最大化学生的词汇量提升。
.png)